Linux Kernel Load Average计算分析

这篇文章是我对于Linux Kernel Load Average计算的个人理解，因为到目前为止，我还是没有完全搞明白。我搜索了网上很多文章，依然没有搞明白，主要原因有三个，一是我的数学知识基础很差，很多文章中提到的数学公式转换我看不明白(有些甚至是错误的);另外一个是看英文资料比较费劲(尽管我一直努力装作能看懂^_^);第三，很多介绍Linux Kernel Load Average计算的文章重点介绍的是当前活跃进程数是如何得到的，并没有介绍load在一段时间内的平均值是怎么计算。尽管如此，经过一段时间的学习和探讨，对于计算Load Average过程已经理解部分我觉得还是有必要记录下来。

load是系统负载很重要的一个指标，top, uptime, w三个命令都能查看系统在前1min, 5min, 15min中的load平均值(Load Average), 但是Linux Kernel对于load一段时间内的平均值计算和打印却很复杂。主要原因我认为有两个:

1.load的计算实际上使用的是数学概率和统计中时间序列预测法中的指数平滑法;
2.Linux Kernel不能直接做浮点运算(Floating-point arithmetic),只能做定点运算(Fixed-point arithmetic),如果不了解定点运算，Linux Kernel Load Average的代码更难理解。

所以核心的两点是要先了解什么是指数平滑法和定点运算。

1.指数平滑法(Exponential smoothing)

指数平滑法是布朗(Robert G..Brown)所提出，指数平滑法常用于生产预测，比如中短期经济发展预测。最简单的预测方法全期平均法把历史一段时间的值求平均数，使用这个平均数去预测下一个时间段的发展趋势，这种预测方法需要对历史数据一个不漏地全部加以同等利用，并且这种预测方法适用于预测对象变化较小且无明显趋势。另外一种称作移动平均法，这种预测方法不考虑远期数据(移动平均法具体的细节没有了解过:) )。指数平滑法兼容了全期平均法和移动平均法所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度。指数平滑的基本公式如下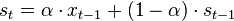： exponential_smoothing_formula [0<α<1]

S_t :时间t的平滑均值。
X_t-1 :时间t-1的实际值。
S_t-1 :时间t-1的平滑均值。
α :平滑常数(平滑因子)。

从上面的公式可以看出，要预测t时刻的平滑均值S_t只要得到t-1时刻的平滑均值S_t-1和t-1时刻的当前值X_t-1,α是一个平滑常数(有时称作平滑因子)，α是一个常量[0<α<1]，α的选取对于指数平滑公式的准确度很重要，当α越趋近于1，S_t-1对于S_t的影响就越小，X_t-1对于S_t的影响就越大，反之亦然。α的选取往往是从历史数据中提取出来。S_t-1可以扩展成S_t-1 = α * X_t-2 + (1 – α) * S_t-2，并且S_t-n可以继续扩展下去，直到n=0,由此可以得出历史预测值S_t-n n越小对于当前S_t的影响就越小，这是一个衰减的过程。

指数平滑又分为一次指数平滑，二次指数平滑和三次指数平滑。一次指数平滑和指数平滑的基本公式没有区别，我们也只考虑这种情况。这种预测方法的好处是它既不需要存储全部历史数据，也不需要存储一组数据。

有时通过一段时间的收集发现平滑指数的预测偏离了实际的数值，需要通过趋势调整，添加一个趋势修正值，可以一定程度上改进指数平滑预测结果，调整后的指数平滑公式为:

S_t = α * X_t-1 + (1 – α) * S_t-1 + T_t， [0 < α < 1]

T_t也是通过一段时间的历史数据计算得来的一个值，具体我们就不深究了。

Linux Kernel对于load 均值的计算是在时钟中断里面完成，所以要求尽快完成，能存储的历史数据自然是有限。历史数据越多，运算花费的时间就越多，简而言之，就是处理越快越好！指数平滑法能很好应用到load均值计算中，它要求存储的历史数据很少，并且平滑因子选取正确就能正确计算出load的均值。但是Linux Kernel对于load均值的计算不是预测未来，而是计算这一时刻前1min, 5min, 15min的平滑均值。以1min为例，指数平滑公式是预测未来1min的平滑均值，而Linux Kernel要通过当前时刻值和1min之前的平滑均值来计算最近1min的平滑均值。Linux Kernel给出了自己的计算公式，这种数学上的变换对于我这种数学基础很差的人来说是理解不了的。(^_^!! 如果你知道是如何变换的，请邮件给我告知，谢谢！)，Linux Kernel的计算公式是:

load_t = load_t-1 * α + n * (1 – α)，[0 < α < 1]

这是linux-2.6.18里的load均值计算公式，在最近版本(3.12)的linux kernel中，load均值的计算公式中增加了一个很小的趋势修正值z(没弄明白为啥。)。公式如下：

load_t = load_t-1 * α + n * (1 – α) + z，[0 < α < 1]

n表示当前进程数(实际上是RUNNABLE状态和TASK_UNINTERRUPTIBLE状态的进程数)。
load_t表示当前时刻一段时间内的平滑均值。
load_t-1表示上一时间段的平滑均值。
α的选取又是一个以我的数学基础不能理解的值，貌似跟电容里面的充电和放电过程类似，(学通信和信号处理的同学应该清楚些)。 Linux Kernel要计算的是前1min, 5min, 15min的Load 均值，α需要分别选取。Linux Kernel选取的是: e^-5/(60*m)
5:表示5s，作分子。
60:表示60s。
m: 表示分钟，1, 5, 15。 60 * m作为分母。
把m带入到公式计算，分别能计算出0.920044415，0.983471454，0.994459848，这三个值我们先记下，后面还会用到。

是不是到目前为止就能完全理解Linux Kernel对于Load均值的计算过程呢，NO!。Linux Kernel 不能做浮点运算，不能直接在内核里面定义float或double类型的变量，而load是一个需要有小数的值，并且[0 < α < 1]也是小数,所以Linux Kernel不能直接运用公式。

2.定点运算(Fixed-point arithmetic)

定点运算是相对于浮点计算(Floating-point arithmetic)来说的。浮点数和定点数只是针对小数点而言，小数点是浮动的就是浮点数，小数点是固定的，就是定点数。有些架构本身就不支持浮点运算单元(FPU),比如有些DSP芯片。当遇到在不支持或者不能使用浮点运算的环境时，浮点运算转换成定点运算，因为定点运算使用的是整数。使用定点数首先需要指定小数点的地方，比如指定一个数的低3位表示小数。举个例子：1500是一个定点数，这个定点数的低3位表示小数，也就是定点数1500相当于浮点数的1.500。在10进制中，浮点数转换成定点数，只要把浮点数*10ⁿ(n表示定点数的小数位数)。比如定点数的小数部分的位数是3位,那么浮点数1.500的定点表示就是1.500 * 10³ = 1500; 如果是浮点数精度位数大于定点数中小数的位数，精度将被丢弃，比如1.5005, 1.5005 * 10³ = 1500的定点数。也就是定点数中小数的位数就是小数的精度。对于二进制数而言其实也是一样的，比如一个32位的定点数，低11位表示存放小数，那边低11位就是二进制数的小数精度。

现在继续考虑定点数的运算加减乘除。还是以10进制数为例，浮点数0.5转换成3位精度的定点数为0.5 * 10³ = 500。当两个浮点数相加时0.5 + 0.5 = 1.0 转换成定点计算应该是500 + 500 = 1000, 结果1000还是一个定点数，定点数1000转换回浮点数的时候1000 / 10³ = 1。加法的运算没有问题，同样减法也是没有问题的。如果是乘法会是怎样呢？浮点数0.5 * 0.5 = 0.25，转换成定点数 500 * 500 = 250000,结果250000却不是我们想要的值，因为250000转换成浮点数时250000 / 10³ = 250, 所以定点乘法运算要进行一定的修正，修正的方法是在乘法的结果上除以10³,所以定点数的乘法运算方式是 (500 * 500) / 10³。若是除法，则刚好和乘法相反，浮点数0.5 / 0.02 = 25 转换成定点运算500 / 20 = 25，定点数25再转换成浮点数便是0.025, 而实际浮点计算的结果是25,所以除法运算的方式是 (500 / 20 ) * 10³ = 25000,这样在转换回浮点数的时候就是正确的。

虽然是以10进制为例，但是在2进程中的运算也是一样的。定点运算总结出来的结果就是：
1.定点数的加法和减法是可以直接进行的。
2.定点数的乘法需要在乘法运算的结果之后除以bⁿ(b:进制， n表示小数的位数)进行修正。
3.定点数的除法需要在除法运算的结果之后乘以bⁿ(b:进制， n表示小数的位数)进行修正。

3.Linux Kernel Load Average计算公式推导

经过前面对于指数平滑法和定点运算的分析，我们再来推导Linux Kernel Load Average的计算方式。首先Linux Kernel对于load 1min,5min,15min之前的load均值计算公式如下：
load_t = load_t-1 * α + n * (1 – α)，[0 < α < 1]
平滑常量α对应于1min,5min,15min分别是0.920044415,0.983471454,0.994459848。

前面说了，这个公式不能直接在Linux Kernel里面用浮点数的方式计算出来，那么只能把上面的公式通过定点数来计算。以1min的计算过程为例,小数位数为2进制的11位。
1.首先需要把平滑常量α 0.920044415转换成定点数：0.920044415 * 2¹¹ = 1884.
2.当前进程数n和常数1也要转换成定点数: n * 2¹¹, 1 * 2¹¹。
3.浮点运算 n * (1 – α) 就转换成了 ((n * 2¹¹) * ((1 * 2¹¹) – 1884)) / 2¹¹ 。
4.load_t-1 * α 转换稍微有点特殊，当t=1时，load_t-1 = load₀，也就是load的最初始值，如果load的最初始值为0,那么定点数和浮点数表示都是一样的，如果load最初始值大于0,首先需要把load最初始值转换成定点数。所以load_t-1本身就是定点数不需要转换。最终转换成 (load_t-1 * 1884) / 2¹¹。
5.整个公式就转换成了:
load_t * 2¹¹ = (load_t-1 * 1884 + (n * 2¹¹) * ((1 * 2¹¹) – 1884)) / 2¹¹。

4.Linux Kernel Load Average的计算和打印代码分析

现在，是时候去看看Linux Kernel代码，Kernel实际是怎么做的。首先内核定义了一些宏。

include/linux/sched.h

158 #define FSHIFT      11      /* nr of bits of precision */
159 #define FIXED_1     (1<<FSHIFT) /* 1.0 as fixed-point */
160 #define LOAD_FREQ   (5*HZ+1)    /* 5 sec intervals */
161 #define EXP_1       1884        /* 1/exp(5sec/1min) as fixed-point */
162 #define EXP_5       2014        /* 1/exp(5sec/5min) */
163 #define EXP_15      2037        /* 1/exp(5sec/15min) */

FSHIFT定义的是定点运算中11位表示小数的精度; FIXED_1就是定点数的1.0; EXP_1, EXP_5, EXP_15分别表示平滑常数的α的定点数表示。根据指数平滑公式，平滑常数α确定之后，只要知道历史的平滑均值和当前的实际值，就能计算出当前的平滑均值。Linux Kernel每5s计算一次, LOAD_FREQ定义的就是5s。接着看代码：

kernel/sched/proc.c
65 /* Variables and functions for calc_load */
66 atomic_long_t calc_load_tasks;
67 unsigned long calc_load_update;
68 unsigned long avenrun[3];
69 EXPORT_SYMBOL(avenrun); /* should be removed */
......
101 /*
102  * a1 = a0 * e + a * (1 - e)
103  */
104 static unsigned long
105 calc_load(unsigned long load, unsigned long exp, unsigned long active)
106 {
107     load *= exp;
108     load += active * (FIXED_1 - exp);
109     load += 1UL << (FSHIFT - 1);
110     return load >> FSHIFT;
111 }
......
346 /*
347  * calc_load - update the avenrun load estimates 10 ticks after the
348  * CPUs have updated calc_load_tasks.
349  */
350 void calc_global_load(unsigned long ticks)
351 {
352     long active, delta;
353
354     if (time_before(jiffies, calc_load_update + 10))
355         return;
356
357     /*
358    * Fold the 'old' idle-delta to include all NO_HZ cpus.
359     */
360     delta = calc_load_fold_idle();
361     if (delta)
362         atomic_long_add(delta, &calc_load_tasks);
363
364     active = atomic_long_read(&calc_load_tasks);
365     active = active > 0 ? active * FIXED_1 : 0;
366
367     avenrun[0] = calc_load(avenrun[0], EXP_1, active);
368     avenrun[1] = calc_load(avenrun[1], EXP_5, active);
369     avenrun[2] = calc_load(avenrun[2], EXP_15, active);
370
371     calc_load_update += LOAD_FREQ;
372
373     /*
374     * In case we idled for multiple LOAD_FREQ intervals, catch up in bulk.
375     */
376     calc_global_nohz();
377 }

首先看到68行的avenrun定义，这是一个类型为unsigned long大小为3的数组，分别用于存放1min, 5min, 15min的load均值，由于avenrun定义的全局变量，内核编译时会初始化为0，所以avenrun[0], avenrun[1], avenrun[2]的运行时初始值都为0。calc_global_load()对avenrun的值进行计算，354行表示如果LOAD_FREQ(5s)没有消耗掉，就直接退出，也就是统计的周期是5s,(354行代码里面加10的原因函数开头的注释已经说明了),load均值计算完成之后，371行对calc_load_update更新，加上LOAD_FREQ。calc_load_tasks存放的是RUNNABLE和TASK_UNINTERRUPTIBLE进程的数量，这个值在calc_global_load()之外更新，364行读取calc_load_tasks到active,365行把active转换成定点数表示。367，368和369行就是分别对1min,5min,15min的load均值计算，计算的过程都是调用calc_load()。

calc_load()就是我们上面分析的指数平滑公式的定点运算方法。此时已经基本清楚了Linux Kernel对于load均值的计算方式，下面再看下Linux Kernel如何从定点数中把load的均值打印成浮点形式，不仅如此，我们知道top命令的输出，小数点是之后是有两位的，也就是小数点之后2位还需要做4舍5入。具体代码如下：

fs/proc/loadavg.c
10 #define LOAD_INT(x) ((x) >> FSHIFT)
11 #define LOAD_FRAC(x) LOAD_INT(((x) & (FIXED_1-1)) * 100)
12
13 static int loadavg_proc_show(struct seq_file *m, void *v)
14 {
15     unsigned long avnrun[3];
16
17     get_avenrun(avnrun, FIXED_1/200, 0);
18
19     seq_printf(m, "%lu.%02lu %lu.%02lu %lu.%02lu %ld/%d %d\n",
20         LOAD_INT(avnrun[0]), LOAD_FRAC(avnrun[0]),
21         LOAD_INT(avnrun[1]), LOAD_FRAC(avnrun[1]),
22         LOAD_INT(avnrun[2]), LOAD_FRAC(avnrun[2]),
23         nr_running(), nr_threads,
24         task_active_pid_ns(current)->last_pid);
25     return 0;
26 }

宏LOAD_INT(x)用作取定点数x整数部分，宏LOAD_FRAC(x)用于取定点数x小数部分的10进制的两位，(x) & (FIXED_1-1)就是取到定点数x的小数部分， (x) & (FIXED_1-1) * 100使得小数部分10进制的两位溢出到整数部分，再调用LOAD_INT就能把溢出到整数的10进制2位取出来。4舍5入又是怎么实现的呢？ FIXED_1/200实际上是小数0.005的定点表示，假如load均值小数部分是0.00x,x>=5 0.00x + 0.005就会往高位进1,否则没有影响。最后看下get_avenrun的实现：

kernel/sched/proc.c
79 void get_avenrun(unsigned long *loads, unsigned long offset, int shift)
80 {
81     loads[0] = (avenrun[0] + offset) << shift;
82     loads[1] = (avenrun[1] + offset) << shift;
83     loads[2] = (avenrun[2] + offset) << shift;
84 }

5.参考资料(References)

http://wiki.mbalib.com/wiki/%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95 (指数平滑)
http://en.wikipedia.org/wiki/Exponential_smoothing
http://bbs.ednchina.com/BLOG_ARTICLE_1899924.HTM (定点运算)
http://en.wikipedia.org/wiki/Fixed-point_arithmetic
http://en.wikipedia.org/wiki/Load_(computing)
http://www.teamquest.com/pdfs/whitepaper/ldavg1.pdf
http://www.teamquest.com/pdfs/whitepaper/ldavg2.pdf
http://www.teamquest.com/pdfs/whitepaper/ldavg3.pdf
http://www.eecs.berkeley.edu/Pubs/TechRpts/1987/CSD-87-353.pdf
http://luv.asn.au/overheads/NJG_LUV_2002/luvSlides.html
http://ilinuxkernel.com/?p=869

Bryton's Blog

Bryton Lee 的技术博客